AGOSTO

SEMANA 1

FUNCIONES VECTORIALES DE VARIABLE REAL

REQUISITOS:

Aprender definiciones de funciones, dominio recorrido, definición de limites y propiedades y parámetros de vectores como unitarios, vector proyección  producto escalar y vectorial respectivamente.

En esta semana  Aprendimos a cambiar de una una función F en los reales a ecuaciones parametricas, cartesianas; tambien se realizo ejercicios de estos y se vio propiedades de los limites aplicados en los vectores. También realizamos ejercicios de vectores (algo sencillo). 

Me di cuenta que es muy parecido a los vectores solo que con otra notación expresada con funciones y que también que existe modulo, producto punto y producto vectorial aplicados en estas propiedades donde un producto cruz nos sirve para sacar un vector perpendicular al plano y perpendicular a los vectores que están en el plano.

Propiedades de límites:  Sean n un entero positivo, k una constante y f,g funciones que tengan límites en c.  Entonces:

Observación: En caso de tener una función en parámetros de t"; entonces para cambiar a una ecuación cartesiana solo se puede hacer eliminando el parámetro "t" y dejando en función de "x" y "y" o "z" según sea el caso.

SEMANA 2

LIMITES 

REQUISITOS:

Saber identidades trigonométricas, propiedades de los limites, y como resolverlos, tener conocimientos básicos de continuidad y como resolver integrales y tener conocimientos de vectores y sus parámetros.

Recuerda: Las siguientes identidades trigonométricas:

Ejemplo de Continuidad

Ahora estas son las mismas definiciones anteriores solo que ahora estamos trabajando en vectores de los cuales solo cambian en mas parámetros pero sigue siendo la misma forma de resolver solo que utilizamos un sistema de coordenadas los cuales son representados por i, j y k.

La derivada

PROPIEDADES

FORMULAS DE INTEGRAL BÁSICAS:

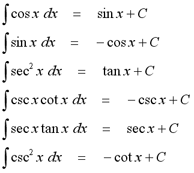
PROPIEDADES 

 OBSERVACIÓN: Todo se resuelve de igual manera que antes solo que ahora se denota en forma de vector ( solo con i, j, k).

APLICACIONES GEOMÉTRICAS

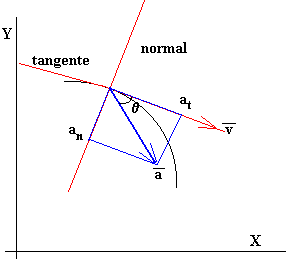
NOTA: ES MUY APLICADO EN FÍSICA

SEMANA 3

PLANO OSCILADOR

Es un vector generado por los vectores normal y tangencial vistos anteriormente

Vector Tangente, Vector Normal y Vector Binormal

La tangente de una curva es una recta que intersecta la curva en un solo punto. Es conocido por nosotros a través del cálculo que mediante la diferenciación de una función se obtiene el punto tangencial para la curva de esa función. Un concepto similar es aplicable al cálculo vectorial, junto con una excepción.

Para una función con un vector de la forma, (x), un vector de la forma es llamado vector tangente en el caso de que esta función sea real y su magnitud no sea igual a cero. En esta situación, la tangente de la función dada (x) en un punto arbitrario es paralela al vector tangente, en ese punto. Aquí, con el fin de tener un vector tangente, 0 es un pre-requisito esencial. Esto es debido a que un vector de magnitud cero no puede tener dirección.

De manera similar, un vector tangencial unitario es definido como,

Aquí s es la longitud total del arco dado, (t) es el vector posición de la función dada y t es la variable de parametrización.

En la figura anterior, X es un punto estático, mientras que P es un punto en movimiento. El punto P se mueve lentamente en la dirección del punto X, mientras el punto P se acerca al punto X, el vector desde el punto X hasta el punto P se acerca al vector tangente en el punto X. La recta que contiene el vector tangente se conoce como recta tangencial.

Un vector normal es algo similar a un vector unitario, suponga que para una función (x), (t) es el vector posición, entonces el vector normal para la función dada es definida como,

Aquí es el vector unitario de la función dada.

Como se describió en la figura anterior, un vector normal es un vector que está perpendicular a un plano o superficie dada. Un vector normal para una superficie dada en un punto arbitrario,sea (x, y), 

Donde la ecuación del plano es,

f(x, y, z) = ax + by + cz + d = 0

Un vector binormal es un producto cruz o producto vectorial del vector normal y del vector unitario normal. Suponga que para una función (x), (t) es el vector posición, entonces el vector binormal para la función dada se define como,

Como sabemos que tanto un vector unitario como un vector normal son vectores unitarios y que se encuentranperpendicular a la superficie dada, un vector Binormal es también un vector unitario que se encuentra normal a un plano o superficie dada. Este vector es normal a ambos, el vector unitario y el vector normal.

SEMANA 3

TRIEDRO MÓVIL

REQUISITOS: Entender lo anterior dado y resolver sin problema alguno lo que es derivadas e integrales. Saber las propiedades vectoriales.


Se llama triedro móvil al triedro formado por vectores unidad (vectores) que acompaña el movimiento de un punto por una curva en el espacio 3D, en contraposicion al triedro fijo con vectores i , j , k
El primer vector (t : tangente) se ubica sobre la tangente de la curva en la dirección  de la primera derivada del vector posición , el segundo vector (n : normal) sobre la normal en la dirección de la segunda derivada del vector posición, el tercer vector (b : binormal) es el producto vectorial
de los otros dos (t x n)

LONGITUD DE ARCO

Como su nombre lo dice sirve para calcular una longitud de curva en un intervalo dado y esta representado por




NOTA: circulo y circunferencia son muy diferentes ya que circulo es la región dada y curvatura en simplemente el arco pero no la región